XJTU System Optimization and Scheduling Midterm Report

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 6.5k 阅读时长 ≈ 6 分钟

Midterm Report

西安交通大学《系统优化与调度》课程中期报告

Problem

\[ min\ \ x_1^3+x_2^3-2x_1^2x_2+5x_1x_2^2+10x_1x_2+7x_1-x_2\\ s.t.\left\{ \begin{array}{**lr**} -x_1+x_2\leq0\\ -2x_1-5x_2-10\leq0\\ x_1-100\leq 0 \end{array} \right. \]

The graph of the object function is shown below:

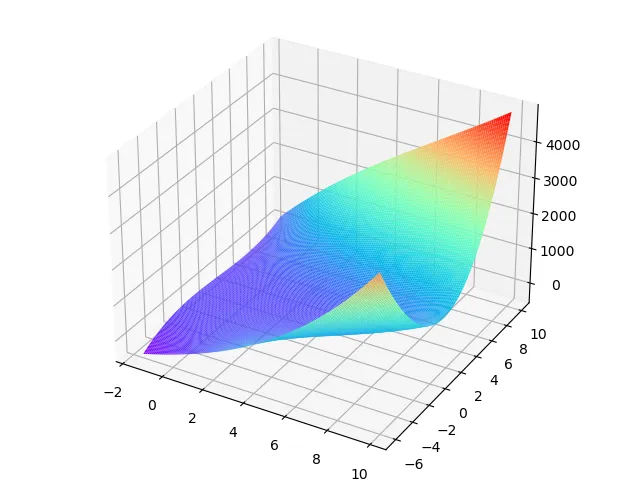
object function

The feasible region by the constraint is shown blow:

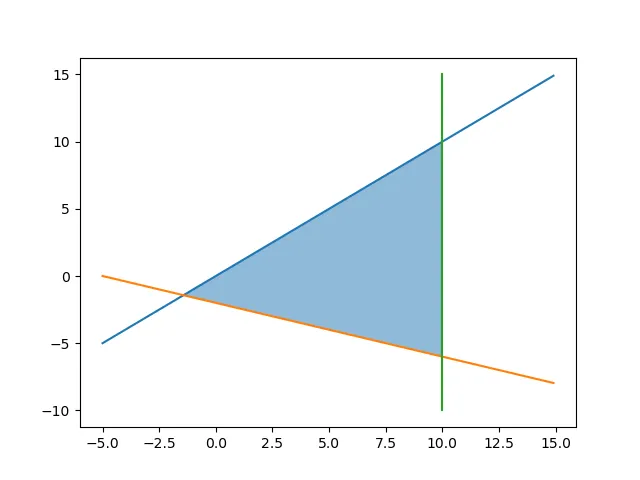
constraint

Method

For this problem, we can see that the feasible region is a convex set, and the object function is not convex. Considering the feasible region, the constraint works only when searching out the boundary. Using projection method could let the searched point outing the boundary move to the boundary. So the method I using is below:

  1. choose the start point \(x^0\)
  2. replace point with the projection\([x^0]^+\)
  3. get the projection of next direction point \(\bar x_k=[x^k-\nabla f(x^k)]^+\)
  4. get the search direction \(d^k=\bar x^k-x^k\)
  5. calculate the next point \(x^{k+1}=x^k+\alpha^kd^k\)
  6. if the terminal condition is satisficed, stop the search and output the result, else go to the step 3

In this project, I choose Armjio rule to control the step size.

The parameters of the method is following: \[ s=1\ \ \beta=0.5\ \ \sigma=1e-5 \]

Solution

Considering the floating error of computers, stipulate \(a=b\) when \(|a-b|<\varepsilon\), and \(a=0\) if \(|a|<\varepsilon\). In this project, \(\varepsilon=1e-19\).

choose the start point (0,0), we could get the following answer:

\(x^k\) \(f(x^k)\) \(\alpha^k\) \(d^k\)
1 （0,0） 0 1 (-1.42857,-1.42857)
2 (-1.42857,-1.42857) -2.74052 1 (1.71358,-0.68543)
3 (0.28501,-2.11400) -4.62839 0.5 (-1.71358,0.68543)
4 (-0.57178,-1.77129) -5.65909 0.25 (2.55462,-1.02185)
5 (0.06688,-2.02675) -5.79388 0.25 (-1.49545,0.59818)
6 (-0.30699,-1.87721) -6.20808 0.125 (0.86671,-0.34668)
7 (-0.19865,-1.92054) -6.25856 0.125 (-0.08902,0.03561)
8 (-0.20977,-1.91609) -6.25903 0.125 (0.01624,-0.00649)
9 (-0.20775,-1.91690) -6.25904 0.125 (-0.00284,0.00114)
10 (-0.20810,-1.91676) -6.25904 0.125 (0.00050,-0.00020)
11 (-0.20804,-1.91679) -6.25904 0.125 (-0.00009,0.00004)
12 (-0.20805,-1.91678) -6.25904 0.125 (0.00002,-0.00001)

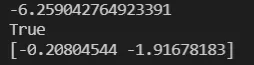
The final result is \(x^*=[-0.20805, -1.91678],f(x^*)=-6.25904\).

same as the result solved by the python package scipy.optimize.minimize:

image-20211222010030267

Change the start point to (5,-8), and the answer following:

\(x^k\) \(f(x^k)\) \(\alpha^k\) \(d^k\)
1 (6.37931,-4.55172) 955.45385 1 (-7.80788,3.12315)
2 (-1.42857,-1.42857) -2.74052 1 (1.71358,-0.68543)
3 (0.28501,-2.11400) -4.62839 0.5 (-1.71358,0.68543)
4 (-0.57178,-1.77129) -5.65909 0.25 (2.55462,-1.02185)
5 (0.06688,-2.02675) -5.79388 0.25 (-1.49545,0.59818)
6 (-0.30699,-1.87721) -6.20808 0.125 (0.86671,-0.34668)
7 (-0.19865,-1.92054) -6.25856 0.125 (-0.08902,0.03561)
8 (-0.20977,-1.91609) -6.25903 0.125 (0.01624,-0.00649)
9 (-0.20775,-1.91690) -6.25904 0.125 (-0.00284,0.00114)
10 (-0.20810,-1.91676) -6.25904 0.125 (0.00050,-0.00020)
11 (-0.20804,-1.91679) -6.25904 0.125 (-0.00009,0.00004)
12 (-0.20805,-1.91678) -6.25904 0.125 (0.00002,-0.00001)

We can see that the searching point went to the boundary quickly, and then the trajectory of the searching is same as ahead.

Appendix

1
2
language: python
package: numpy, matplotlib, scipy

The source code is following:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
from math import sqrt
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.optimize import minimize

# 小于该数则判断为0
epsilon=1e-19

# 自动求梯度
def autograd(f,*args):
    delta=1e-9
    var_num=len(args)
    grads=[]
    # 计算当前函数值
    func_value=f(args)
    for i in range(var_num):
        # 计算偏移后的变量
        args_new=list(args)
        args_new[i]+=delta
        args_new=tuple(args_new)
        # 计算偏移后函数值
        delta_func_value=f(args_new)
        # 求偏导
        partial=(delta_func_value-func_value)/delta
        grads.append(partial)
        
    return tuple(grads)

# 定义函数
f=lambda x: x[0]**3+x[1]**3-2*x[0]**2*x[1]+5*x[0]*x[1]**2+10*x[0]*x[1]+7*x[0]-x[1]
g1=lambda x: x[0]-x[1]
g2=lambda x: 2*x[0]+5*x[1]+10
g3=lambda x: -x[0]+10

line1=[(10,-6),(10,10)]
line2=[(-2/1.4,-2/1.4),(10,10)]
line3=[(-2/1.4,-2/1.4),(10,-6)]

# 计算凸包上的最近距离点
def get_closest_point(x,y,line):
    if line[0][0]==line[1][0]:
        px=line[0][0]
        py=y
        if py>line[1][1]:
            py=line[1][1]
        if py<line[0][1]:
            py=line[0][1]
    else:
        k=(line[0][1]-line[1][1])/(line[0][0]-line[1][0])
        b=line[0][1]-k*line[0][0]
        px=(y+x/k-b)/(k+1/k)
        py=k*px+b
        if px<line[0][0]:
            px=line[0][0]
            py=line[0][1]
        if px>line[1][0]:
            px=line[1][0]
            py=line[1][1]
    
    distance=sqrt((x-px)**2+(y-py)**2)
    return distance,(px,py)

# 计算点(x,y)在凸包上的投影
def project(x,y):
    if g1([x,y])>=0 and g2([x,y])>=0 and g3([x,y])>=0:
        return (x,y)
    d1,p1=get_closest_point(x,y,line1)
    d2,p2=get_closest_point(x,y,line2)
    d3,p3=get_closest_point(x,y,line3)
    if d1==min(d1,d2,d3):
        return p1
    if d2==min(d1,d2,d3):
        return p2
    if d3==min(d1,d2,d3):
        return p3

# 投影最速下降法
def steepest_method(f,*start_point):
    s=1
    beta=0.5
    m=0
    sigma=1e-5
    point=np.array(project(*start_point))
    
    while(True):
        last_point=point
        # 计算函数值
        value=f(point)
        # 计算梯度
        grad_f=autograd(f,*point)
        
        # 检查是否达到终止条件
        is_solve=True
        for grad in grad_f:
            if abs(grad)>epsilon:
                is_solve=False
        # 如果精度达到终止条件，则停止并返回当前点
        if is_solve:
            break
        # 否则继续向下运算
        point=point-grad_f
        # 对点进行投影
        point=project(*point)
        # 计算更新方向
        direction=point-last_point
        
        # 计算下一个搜索点
        point=last_point
        # Armijo准则选择步长
        while True:
            alpha=beta**m*s
            new_point=point+alpha*direction
            d_sum=0
            for i,d in enumerate(direction):
                d_sum+=grad_f[i]*d
            if f(point)-f(new_point)>=-sigma*alpha*d_sum:
                point=new_point
                break
            m+=1
        # 打印日志
        print('x_k:({:.5f},{:.5f}) f: {:.5f} a: {:.5f} d: ({:.5f},{:.5f})'.format(last_point[0],last_point[1],f(last_point),alpha,direction[0],direction[1]))
        point=last_point+alpha*direction
        
        # 如果迭代步长很小，则停止迭代
        err=0
        for i in range(len(point)):
            err+=abs(point[i]-last_point[i])
        if err<1e-5:
            break
    # 对结果保留5位小数
    ans=[]
    for p in point:
        ans.append(round(p,5))
    return ans,f(ans)
    
print(steepest_method(f,5,-8))

######################
# 绘图
x=np.arange(-5,15,0.1)
y1=x
y2=-0.4*x-2

plt.plot(x,y1)
plt.plot(x,y2)
plt.plot([10,10],[-10,15])
plt.fill_between(x,y1,y2,where=(x<10)&(y1>y2),alpha=0.5)
plt.savefig('constraint.png?x-oss-process=style/webp')


figure = plt.figure()
ax = Axes3D(figure)#设置图像为三维格式
X = np.arange(-1.5,10,0.1)
Y = np.arange(-6,10,0.1)#X,Y的范围
X,Y = np.meshgrid(X,Y)#绘制网格
Z=f([X,Y])
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap='rainbow')
#绘制3D图，后面的参数为调节图像的格式
plt.savefig('obj_func.png?x-oss-process=style/webp')
#######################

# scipy求解验证结果正确性

cons=({'type':'ineq','fun':g1},
      {'type':'ineq','fun':g2},
      {'type':'ineq','fun':g3})


x0 = np.asarray((0,0))
res=minimize(f,x0,method='SLSQP',constraints=cons)
print(res)