Vanilla Policy Gradient关于loss mean与sum的探讨

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 4.2k 阅读时长 ≈ 4 分钟

最近在逐一复现RL算法过程中，策略梯度算法的收敛性一直有问题。经过一番探究和对比实验，学习了网上和书本上的很多实验代码之后，发现了代码实现中的一个小问题，即Policy Gradient在计算最终loss时求平均和求和对于网络训练的影响，本文将对此进行展开讨论。

先说结论：

在进行策略梯度下降优化策略时，可以对每个动作的loss逐一（for操作）进行反向传播后进行梯度下降，也可以对每个动作的loss求和（sum操作）之后进行反向传播后梯度下降，但尽量避免对所有动作的loss求平均（mean操作）之后进行反向传播后梯度下降，这会导致收敛速度较慢，甚至无法收敛。

具体的论证和实验过程见下文。

Vanilla Policy Gradient简介

Vanilla Policy Gradient(VPG, i.e. REINFORCE)，中文译为策略梯度算法。是策略优化的经典算法。首先进行一些符号说明：

  • \(s_t\): 环境在\(t\)时刻的状态
  • \(a_t\): 智能体在\(t\)时刻选择的动作
  • \(\pi_\theta\): 智能体的策略，在这里由参数为\(\theta\)的神经网络表示
  • \(\pi_\theta(a|s)\): 智能体在状态\(s\)时选择动作\(a\)的概率
  • \(r_t\): 环境在\(t\)时刻给出的奖励
  • \(\gamma\): 折扣因子
  • \(g_t\): 累计折扣奖励，\(g_t=\sum_{t'=t}^T \gamma^{t'-t}r_t\)

VPG的大致分为两步：收集经验和优化策略。两部分的具体实现如下：

  1. 智能体与环境进行交互，直到一个episode终止，获得一系列轨迹\(s_1,a_1,r_1,s_2,a_2,r_2...s_n,a_n,r_n\)
  2. 对\(\theta\)进行更新：\(\theta =\theta +\alpha\nabla_\theta \pi_\theta(a_t|s_t) g_t\)

为何要对loss使用sum和mean

策略梯度算法是一个梯度上升算法，为了便于使用当前的梯度下降框架，采用\(loss = -\nabla_\theta \pi_\theta(a_t|s_t)g_t\)即可。

在VPG算法实现过程中，神经网络的训练部分使用了pytorch框架来进行实现。在该框架中，进行反向传播的loss必须是一个标量。而策略梯度算法对每一时刻的\((s_t,a_t,g_t)\)三元组都会进行一次梯度下降的更新。也就是需要产生多次反向传播，对于该问题主要有三种解决方案：

  1. 对每个时刻的\((s_t,a_t,g_t)\)三元组逐一进行反向传播，最后进行梯度下降，实现代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    batch = self._buffer.sample(0)[0]
    G = 0

    self._optimizer.zero_grad()
    for i in reversed(range(len(reward))):
        r = reward[i]
        state = torch.FloatTensor([batch["obs"][i]]).to(self.device)
        action = torch.LongTensor([batch["act"][i]]).view(-1,1).to(self.device)
        log_prob = torch.log(self._network(state)).gather(1,action)
        G = self._gamma * G + r
        loss = -log_prob * G
        loss.backward()
    self._optimizer.step()

  2. 对所有计算出的\(loss\)进行求和再反向传播，实现代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    batch = self._buffer.sample(0)[0]
    state = torch.FloatTensor(batch['obs']).to(self.device)
    action = torch.LongTensor(batch['act']).to(self.device)
    reward = torch.FloatTensor(batch['rew']).to(self.device)

    # clean gradient
    self.optimizer.zero_grad()
    # computing discount reward
    discount_reward=torch.zeros_like(reward)
    discount_reward[-1]=reward[-1]
    for t in reversed(range(len(reward)-1)):
        discount_reward[t]=reward[t]+self._gamma*discount_reward[t+1]
    # forward computing
    action_probs=self._network(state)
    # computing loss
    loss = -torch.log(action_probs.gather(1, action.view(-1,1)))
    loss = torch.sum(loss*discount_reward.unsqueeze(-1))
    # back propagation
    self.optimizer.step()

  3. 对所有计算出的\(loss\)进行平均再反向传播，实现代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    batch = self._buffer.sample(0)[0]
    state = torch.FloatTensor(batch['obs']).to(self.device)
    action = torch.LongTensor(batch['act']).to(self.device)
    reward = torch.FloatTensor(batch['rew']).to(self.device)

    # clean gradient
    self.optimizer.zero_grad()
    # computing discount reward
    discount_reward=torch.zeros_like(reward)
    discount_reward[-1]=reward[-1]
    for t in reversed(range(len(reward)-1)):
        discount_reward[t]=reward[t]+self._gamma*discount_reward[t+1]
    # forward computing
    action_probs=self._network(state)
    # computing loss
    loss = -torch.log(action_probs.gather(1, action.view(-1,1)))
    loss = torch.mean(loss*discount_reward.unsqueeze(-1))
    # back propagation
    self.optimizer.step()

为何对loss使用sum和mean会导致结果不同

假设一个episode的长度为\(n\)，则会产生\(n\)个经验三元组\((s_1,a_1,g_1),(s_2,a_2,g_2),...,(s_n,a_n,g_n)\)，记每个经验三元组计算出的\(loss\)分别为\(l_1,l_2,...,l_n\)。下面分别对sum和mean对loss反向传播的影响进行分析。

若对\(loss\)进行求和，即\(l_{tot}=l_1+l_2+...+l_n\)，根据链导法则可得： \[ \frac{\partial l_{tot}}{\partial \theta}=\frac{\partial l_1}{\partial \theta}+\frac{\partial l_2}{\partial \theta}+...+\frac{\partial l_n}{\partial \theta} \] 因此，使用\(l_{tot}\)求梯度并进行反向传播相当于每个\(loss\)分别求梯度的累计。

若对\(loss\)进行求平均，即\(\bar l=\frac 1n (l_1+l_2+...+l_n)\)，根据链导法则可得： \[ \frac{\partial \bar l}{\partial \theta}=\frac 1n \bigg(\frac{\partial l_1}{\partial \theta}+\frac{\partial l_2}{\partial \theta}+...+\frac{\partial l_n}{\partial \theta}\bigg) \] 相比于求和，对\(loss\)求平均相当于在梯度传播时多了一个大小为\(\frac 1n\)的常数。

乍一看，对\(loss\)进行求和和求平均操作对梯度反向传播带来的影响只有一个常数项。两者相差不大。然而，问题在于，VPG的每个episode的长度是不固定的。假设进行了\(m\)场episode，长度分别为\(n_1,n_2,n_3,...,n_m\)，那么如果每个episode结束时对\(loss\)求平均，则带来的常数项分别为\(\frac 1{n_1},\frac 1{n_2},\frac 1{n_3},...,\frac 1{n_m}\)。从而给神经网络的训练造成不平稳。

实验对比

实验采用gym中的CartPole-v1环境作为训练环境，训练网络及学习超参数如下：

  • 隐层大小：[128, 128]
  • 优化器：Adam
  • 学习率：3e-4

按照上述参数对\(loss\)循环反向传播，求和反向传播，平均反向传播进行实验，每种传播方式训练10次，训练得到的reward曲线以0.7的系数进行平滑，得到的实验结果如下：

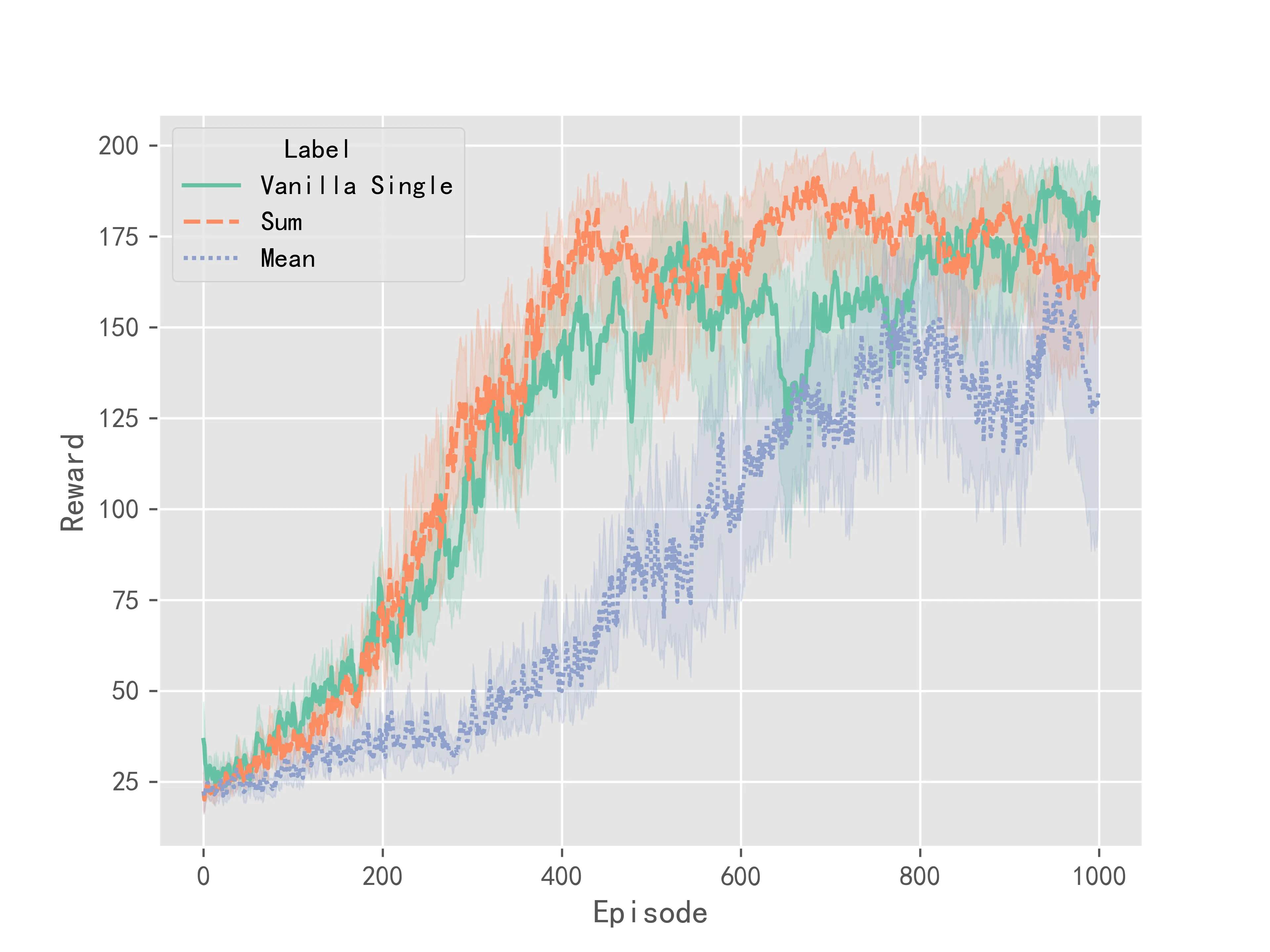
图1 loss循环反向传播，求和反向传播，平均反向传播训练结果对比

总结：由上述实验结果可知，若对\(loss\)求平均之后再进行反向传播，神经网络可能不会收敛到一个好的策略。因此在进行策略梯度算法计算时要尽量避免对\(loss\)取平均的操作。